Question

The ratio v ′ 2 v2 of potential differences across capacitor c2 for the two cases is

Answer 1

The ratio of potential differences across a capacitor is determined by its charge and capacitance and is influenced by how the capacitors are arranged in the circuit.

Step-by-step explanation:

The question seems to be related to the potential difference (voltage) across capacitors when configured in certain electrical circuits, such as in series or parallel arrangements. In general, the potential difference across a capacitor is determined by the charge on the capacitor and its capacitance, as described by the equation V = Q/C, where V is the potential difference, Q is the charge, and C is the capacitance.

When dealing with multiple capacitors, as described, the total voltage across capacitors in series is the sum of the individual voltages, which are each a product of their individual charges and capacitance. Conversely, capacitors in parallel have the same voltage across them. The ratio v'2/v2 calculated across capacitor C2 could be influenced by their configuration in the circuit and any changes made to the circuit such as reconfiguring the capacitors or changing their connections.

Answer 2

The answer is
`(2)/(2+(k-1)\cdot(C1)/(C2))`.

Let’s find the ratio of the potential differences across capacitor C2 for the two cases.

In the first case, we have two identical capacitors connected to a battery with emf V. The potential difference across each capacitor is V/2.

In the second case, a dielectric slab with dielectric constant k fills the gap of capacitor C2. The potential difference across capacitor C2 is now given by:

`V_C2 = V / (1 + (k - 1) * C1/C2)`

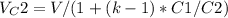
where C1 and C2 are the capacitances of the two capacitors.

The ratio of the potential differences across capacitor C2 for the two cases is:

`V_C2 / (V/2) = 1 / (1 + (k - 1) * C1/C2)`

Simplifying the expression, we get:

`V_C2 / (V/2) = 2 / (2 + (k - 1) * C1/C2)`

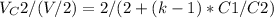
Therefore, the ratio of the potential differences across capacitor C2 for the two cases is 2 / (2 + (k - 1) * C1/C2).

The answer is
`(2)/(2+(k-1)\cdot(C1)/(C2))`.