Question

The equation of a curve is y = A × k^x where A and k are positive constants.

(0, 3.5) and (-1, 1.75) are points on the curve.
Work out the value of A and k.
(4 marks)

Answer 1

y = Ak^x is y=3.5*(2^x)

A = 3.5

k = 2

Explanation:

From point (0,3.5), we can deduce the value of A. Since x is zero, k^x will be 1 [k^0 = 1]. For y to be equal to 3.5, A must be 3.5.

We can now write y = 3.5k^2 and look for the value of k that would produce a value of y = 1.75 with x = -1.

y = 3.5k^x

1.75 = 3.5k^-1

k^-1 = 0.5

k = 2

The equation is y = 3.5*
`2^(x)`

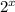
See the attached graph.