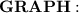
y = -2/3x + 4

To determine which line is perpendicular to line m, we need to find the negative reciprocal of the slope of line m.
The equation of line m is y + 2 = (3/2) (x + 4).
First, let's rearrange the equation into slope- intercept form (y = mx + b) by isolating y:
y + 2 = (3/2)(x + 4)
y + 2 = (3/2)x + 6
y = (3/2)x + 6-2
y = (3/2)x + 4
From the equation, we can see that the slope of line m is 3/2.
The negative reciprocal of 3/2 is -2/3.
Therefore, the line perpendicular to line m will have a slope of -2/3.
Among the given options, the line with the equation y = -2/3x + 4 is perpendicular to line m.