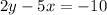Question

Which equation represents a line which is perpendicular to the line y =- +522x - 5y = -302x + 5y = 152y-53 = 10O 5x + 2y 12

Answer 1

The equation that represents the perpendicular line is;

`2y-5x=-10`

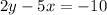
Step-by-step explanation:

We want to find the equation of a line perpendicular to the line;

`y=-(2)/(5)x+5`

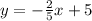
Recall that for two lines to be perpendicular to each other, their slope must be a negative reciprocal of one another.

`m_1.m_2=-1_{}_{}`

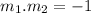
so;

`m_2=-(1)/(m_1)`

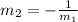
For the given equation, the slope of the given line is;

`m_1=-(2)/(5)`

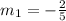
To get the slope of the perpendicular line, let us substitute m1 to the equation above;

`\begin{gathered} m_2=-(1)/(m_1) \\ m_2=-\frac{1}{(-(2)/(5))_{}} \\ m_2=\frac{5}{2_{}} \end{gathered}`

So, the equation of the perpendicular line would be of the form;

`\begin{gathered} y=m_2x+c \\ y=(5)/(2)x+c \\ mu\text{ltiply through by 2} \\ 2y=5x+c \\ 2y-5x=c \end{gathered}`

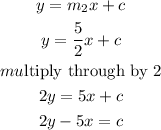
The equation of the perpendicular line will be of the form;

`2y-5x=c`

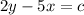
Where c is a constant;

From the options, the only equation that is similar to the derived equation is;

`2y-5x=-10`

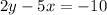
Therefore, the equation of the perpendicular line is;

`2y-5x=-10`