Question

The points (-10,4) and (-6, r) lie on a line with slope 1/4, Find the missing coordinate, r.

Answer 1

r = 5

Explanation:

In order t find the missing coordinate, r, we can use the slope formula:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

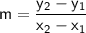
where m is the slope of the line, (x1, y1) is the first point, and (x2, y2) is the second point.

We are given that the slope of the line is 1/4, and the first point is (-10, 4). We are asked to find the missing coordinate, r, of the second point, (-6, r).

Substituting these values into the slope formula, we get:

`\sf (1)/(4) = (r - 4 )/(-6-(-10))`

`\sf (1)/(4) = (r -4 )/(4)`

Multiply both sides by 4.

`\sf (1)/(4) \cdot 4= (r -4 )/(4)\cdot 4`

`\sf 1 = r - 4`

Add 4 on both sides.

`\sf 1 + 4 = r - 4 +4`

`\sf r = 5`

Therefore, the missing coordinate(r), is 5.

Answer 2

r = 5

Explanation:

We know

The slope = (y2 - y1) / (x2 - x1)

m = 1/4

Points: (-10,4) and (-6, r)

Find r.

We substitute the number in the equation.

1/4 =
`((r-4))/((-6-(-10)))`

1/4 =
`((r-4))/(4)`

Multiply both sides by 4

1 = r - 4

r = 5

So, the answer is r = 5