Question

Given that f(x) = x^2 + 14x + 45 and g(x) = x + 9, find f(x) ÷ g(x) and express the result as a polynomial in simplest form.

Answer 1

x + 5

Explanation:

Let's first set up the equation f(x) ÷ g(x)

`(x^(2) + 14x + 45)/(x + 9)`

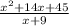
Notice that we can factor the numerator into (x + 9)(x + 5) because adding the two constants [9 + 5] creates the coefficient for the middle term [9 + 5 = 14] for f(x), and multiplying the two constants [9 * 5] creates the constant [9 * 5 = 45] for f(x):

`((x + 9)(x + 5))/(x + 9)`

Now, we can simplify the fraction:

`((x + 9)(x + 5))/(x + 9) = (x + 9)/(x + 9) * (x+5) = 1*(x+5) = x+5`

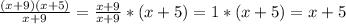
The answer is "x + 5".