Question

Domain of a Function Determine the domain of the two-variable function g(x, y) = 9 / (y + 2x²).

Answer 1

Answer: {x, y ∈ R : y ≠ -2x²}

Step-by-step explanation:

The domain of a function is all possible values of x and y that will make the function true.

The function given is:

`\displaystyle g(x, y) = (9)/(y + 2x^2)`

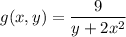
This is a rational function. Here, we can see that the function is undefined when the denominator (y + 2x²) equals 0 since dividing by 0 is undefined.

We can set the denominator (y + 2x²) equal to 0 and solve this equation for y:
y + 2x² = 0
y = -2x²

In mathematical notation, the domain can be expressed as follows:
Domain = {x, y ∈ R : y ≠ -2x²}

This shows that the domain consists of all real numbers where y is not equal to -2x², as these values would make the denominator of the function equal to zero (meaning the rational function is undefined).