Question

Solve for the value of d.
(9d-7)°
(6d+7)°

Answer 1

d=6

Explanation:

It is given that out of the 180 degrees that the angles can add up to, one angle is a right angle.

Because we don't know if the angles are equal, we can add up the angles and subtract it from 180 degrees:

180-(6d+7+9d-7)=90 is our equation. So now we solve:

180-(6d+7+9d-7)=90

Combine like terms:

180-(15d)=90

Add 15d to both sides:

180=90+15d

Subtract 90 from both sides:

15d=90

d=6

Check by plugging in d:

90+6(6)+7+9(6)-7=180

90+36+7+54-7=180

90+43+47=180

90+90=180

It works!

Answer 2

d = 6

Explanation:

A linear pair is a pair of adjacent, supplementary angles. Adjacent angles are angles that share a common vertex and one common arm. Supplementary angles are angles that add up to 180 degrees.

Using this, we can say that:

(9d-7)° + 90° + (6d+7)° = 180°

Simplify like terms:

15d + 90 = 180°

Subtract 90 on both sides.

15d + 90 - 90 = 180 - 90

15d = 90

Divide both sides by 15.

`\sf (15d)/(15)=(90)/(15)`

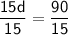
d = 6

Therefore, the value of d is 6.