Question

IxI+1>2
i want to know how they get the infinite sign in the solutions

Answer 1

`\sf x \in (-\infty, -1) \cup (1, \infty)`

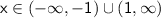
Explanation:

The solutions to the inequality |x|+1>2 are all values of x that make the left-hand side of the inequality greater than 2.

To solve the inequality, we can subtract 1 from both sides:

|x|+1 > 2

|x| > 2 - 1

|x| > 1

This means that the absolute value of x must be greater than 1.

The absolute value of a number is its distance from zero. So, the solutions to the inequality |x| > 1 are all values of x that are more than 1 unit away from zero.

We can represent this on a number line as follows:

... -4 -3 -2 -1 0 1 2 3 4 ...

The solutions to the inequality are all values of `x` that are greater than 1 or less than -1. This can be written mathematically as:

`\sf x > 1 \text{ or } x < -1``

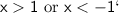
Which can also be written as:

`\sf x \in (-\infty, -1) \cup (1, \infty)`

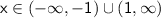
This is why the solutions to the inequality |x|+1 > 2 are written with an infinite sign.