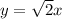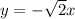Question

(x^2)/9 - (y^2)/18 = 1

Find the center, vertices, foci and asymptotes of the hyperbola


There should be 2 vertices, 2 foci and 2 asymptote equations

Answer 1

`\textsf{Center:}\quad (0,0)`

`\textsf{Vertices:}\quad \left(-3, 0\right)\; \textsf{and}\;\left(3, 0\right)`

`\textsf{Foci:}\quad \left(-3√(3),0\right)\;\textsf{and}\;\left(3√(3),0\right)`

`\textsf{Asymptotes:} \quad y=√(2)x\;,\quad y=-√(2)x`

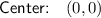
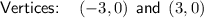
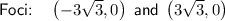
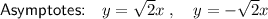
Explanation:

Given equation of the hyperbola:

`(x^2)/(9)-(y^2)/(18)=1`

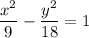
Since the x-term is positive, the hyperbola is horizontal and opens left and right.

The standard equation of a horizontal hyperbola is:

`\boxed{\begin{minipage}{7.4 cm}\underline{Standard equation of a horizontal hyperbola}\\\\$((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center.\\ \phantom{ww}$\bullet$ $(h\pm a, k)$ are the vertices.\\\phantom{ww}$\bullet$ $(h, k \pm b)$ are the co-vertices.\\\phantom{ww}$\bullet$ $(h\pm c, k)$ are the foci where $c^2=a^2+b^2.$\\\phantom{ww}$\bullet$ $y=\pm (b)/(a)(x-h)+k$ are the asymptotes.\\\end{minipage}}`

Comparing the given equation with the standard equation, we have:

• 
  `h = 0`
• 
  `k = 0`
• 
  `a^2 = 9\implies a=√(9)=3`
• 
  `b^2 = 18 \implies b=√(18)=3√(2)`

Therefore, the center (h, k) is located at the origin (0, 0).

To find the coordinates of the vertices, substitute the values of h, k and a into the vertices formula:

`\begin{aligned}\textsf{Vertices}&=(h\pm a, k)\\&=(0\pm 3, 0)\\&=(\pm3,0)\end{aligned}`

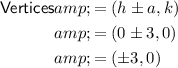
To find the foci, we first need to find the value of c by substituting the values of a² and b² into the equation c² = a² + b²:

`\begin{aligned}c^2&=a^2+b^2\\c&=√(a^2+b^2)\\c&=√(9+18)\\c&=√(27)\\c&=√(3^2 \cdot 3)\\c&=√(3^2) √(3)\\c&=3√(3)\end{aligned}`

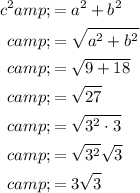
Now, to determine the foci, substitute the values of h, k and c into the foci formula:

`\begin{aligned}\sf Foci&=(h \pm c,k)\\&=\left(0\pm 3√(3),0\right)\\&=\left(\pm 3√(3),0\right)\end{aligned}`

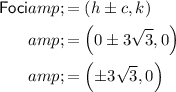
To find the equations of the asymptotes, substitute the values of h, k, a and b into the asymptote formula:

`\begin{aligned}y&=\pm (b)/(a)(x-h)+k\\\\y&=\pm (3√(2))/(3)(x-0)+0\\\\y&=\pm√(2)x\end{aligned}`

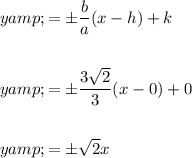
Therefore, the equations of the asymptotes are:

`y=√(2)x`

`y= -√(2)x`