Question

((x-6)^2)/8 - (y^2)/32 = 1

Find the center, vertices, foci and asymptotes of the hyperbola


There should be 2 vertices, 2 foci, and 2 asymptote equations.

Answer 1

Center: (6, 0)

Vertices:

`\sf (6 + 2√(2), 0)`

`\sf (6 - 2√(2), 0).`

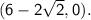
Foci:

`\sf (6 +2√(10), 0)`

`\sf (6 - 2√(10), 0)`

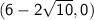
Asymptotes:

y = 2x + 6

y = -2x + 6

Explanation:

`\sf ((x-6)^2 )/(8) -(y^2 )/(32) = 1`

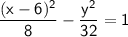
The equation we've given is already in standard form for a hyperbola:

`\sf ((x - h)^2)/(a^2)- ((y - k)^2)/(b^2) = 1`

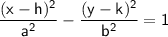
In this equation:

• (h, k) represents the center of the hyperbola.
• 'a' is the distance from the center to the vertices along the x-axis.
• 'b' is the distance from the center to the vertices along the y-axis.

Now, let's identify the key elements of the hyperbola:

Center (h, k): The center of the hyperbola is (h, k), which in this case is (6, 0). So, the center is at (6, 0).

a and b:

From the equation, a² = 8 and b²= 32. Taking square roots, we get:

`\sf a = √(8)= 2√(2)`

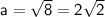
and

`\sf b = √(32)= 4√(2)`

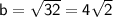
Vertices: The vertices are located along the x-axis at a units to the right and left of the center.

So, the vertices are:

(h ± a,0)

`\sf (6 + 2√(2), 0)` and
`\sf (6 - 2√(2), 0).`

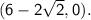
Foci: The distance from the center to each focus is given by c, where c² = a² + b².

In this case,

`\sf c^2 = (2√(2))^2 + (4√(2))^2 = 8 + 32 = 40.`

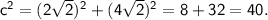
So,

`\sf c = √(40 )= 2√(10.)`

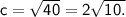
The foci are located at (h + c, k) and (h - c, k), which gives us the foci as
`\sf (6 +2√(10), 0)`and
`\sf (6 - 2√(10), 0).`

Asymptotes: The equations of the asymptotes for a hyperbola centered at (h, k) are given by:

`\sf y - k = \pm (b)/(a)(x-h)`

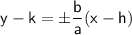
Plugging in the values, we get:

`\sf y - 0 \pm (4 √(2))/(2√(2))(x-h)`

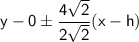
Simplifying, we have:

y = ± 2x + 12

So, the equations of the asymptotes are:

y = 2x + 12

y = -2x + 12

Answer 2

`\textsf{Center:}\quad (6,0)`

`\textsf{Vertices:}\quad \left(6-2√(2), 0\right)\; \textsf{and}\;\left(6+2√(2), 0\right)`

`\textsf{Foci:}\quad \left(6-2√(10),0\right)\;\textsf{and}\;\left(6+2√(10),0\right)`

`\textsf{Asymptotes:} \quad y=2x-12\;,\quad y=-2x-12`

Explanation:

Given equation of the hyperbola:

`((x-6)^2)/(8)-(y^2)/(32)=1`

Since the x-term is positive, the hyperbola is horizontal and opens left and right.

The standard equation of a horizontal hyperbola is:

`\boxed{\begin{minipage}{7.4 cm}\underline{Standard equation of a horizontal hyperbola}\\\\$((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center.\\ \phantom{ww}$\bullet$ $(h\pm a, k)$ are the vertices.\\\phantom{ww}$\bullet$ $(h, k \pm b)$ are the co-vertices.\\\phantom{ww}$\bullet$ $(h\pm c, k)$ are the foci where $c^2=a^2+b^2.$\\\phantom{ww}$\bullet$ $y=\pm (b)/(a)(x-h)+k$ are the asymptotes.\\\end{minipage}}`

Comparing the given equation with the standard equation, we have:

• 
  `h = 6`
• 
  `k = 0`
• 
  `a^2 = 8\implies a=√(8)=2√(2)`
• 
  `b^2 = 32 \implies b=√(32)=4√(2)`

Therefore, the center (h, k) is located at (6, 0).

To find the coordinates of the vertices, substitute the values of h, k and a into the vertices formula:

`\begin{aligned}\textsf{Vertices}&=(h\pm a, k)\\&=(6\pm 2√(2), 0)\end{aligned}`

To find the foci, we first need to find the value of c by substituting the values of a² and b² into the equation c² = a² + b²:

`\begin{aligned}c^2&=a^2+b^2\\c&=√(a^2+b^2)\\c&=√(8+32)\\c&=√(40)\\c&=√(2^2 \cdot 10)\\c&=√(2^2) √(10)\\c&=2√(10)\end{aligned}`

Now, to determine the foci, substitute the values of h, k and c into the foci formula:

`\begin{aligned}\sf Foci&=(h \pm c,k)\\&=\left(6\pm 2√(10),0\right)\end{aligned}`

To find the equations of the asymptotes, substitute the values of h, k, a and b into the asymptote formula:

`\begin{aligned}y&=\pm (b)/(a)(x-h)+k\\\\y&=\pm (4√(2))/(2√(2))(x-6)+0\\\\y&=\pm2(x-6)\\\\y&=\pm2x-12\end{aligned}`

Therefore, the equations of the asymptotes are:

`y=2x-12`

`y= -2x-12`