Question

If f(x) is an exponential function where f(0.5)=1 and f(1.5)=55, then find the value of f(2.5), to the nearest hundredth.

Answer 1

The value of f(2.5) for the given exponential function is approximately 216.81 to the nearest hundredth.

Step-by-step explanation:

Exponential functions are characterized by the form
`\(f(x) = a \cdot b^x\)`, where a is the initial value and b is the base of the exponential function. To find f(2.5), we need to determine the values of a and b using the provided information.

Given that f(0.5) = 1, we can substitute these values into the exponential function:

`\[1 = a \cdot b^(0.5)\]`

Similarly, for f(1.5) = 5:

`\[55 = a \cdot b^(1.5)\]`

Now, by dividing the second equation by the first, we can eliminate a and find the value of b:

`\[b^(1.5) = 55\]`

Taking the cube root of both sides:

`\[b = 55^(1/3)\]`

Now that we know b, we can substitute it back into the first equation to solve for a:

`\[1 = a \cdot (55^(1/3))^(0.5)\]`

Solving for a we find
`\(a \approx 0.372\)`.

Now, with the determined values of a and b, we can find f(2.5) by substituting them into the exponential function:

`\[f(2.5) \approx 0.372 \cdot (55^(1/3))^(2.5)\]`

Calculating this expression gives
`\(f(2.5) \approx 216.81\)`, rounded to the nearest hundredth. Therefore, the value of f(2.5) for the given exponential function is approximately 216.81.

Answer 2

f(2.5) is approximately 219.27 to the nearest hundredth.

To find the value of f(2.5) for the given exponential function, you'll need to determine the equation of the exponential function first. The general form of an exponential function is:

`f(x) = a * b^x`

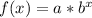
Where:

- f(x) is the function value at x.

- a is the initial value or the value of the function at some specific point (in this case, f(0.5) = 1).

- b is the base of the exponential function.

You have two points on the curve: f(0.5) = 1 and f(1.5) = 55. You can use these points to solve for a and b.

Step 1: Use f(0.5) = 1 to find 'a'.

`1 = a * b^0.5`

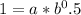
Step 2: Use f(1.5) = 55 to find 'b'.

`55 = a * b^1.5`

Now, you have a system of two equations:

1.
`a * b^0.5 = 1`

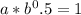
2.
`a * b^1.5 = 55`

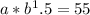
You can solve this system of equations simultaneously. First, divide equation (2) by equation (1) to eliminate 'a':

`(55 / 1) = (a * b^1.5) / (a * b^0.5)`

`55 = b^(1.5 - 0.5)`

`55 = b^1`

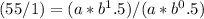
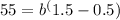
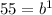
Now, solve for 'b':

`b = 55^(1/1)`

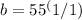
b = 55

Now that you've found 'b,' you can substitute it back into equation (1) to solve for 'a':

`1 = a * 55^0.5`

`a = 1 / 55^0.5`

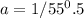
a ≈ 0.1366 (rounded to four decimal places)

Now that you have 'a' and 'b,' you can write the equation of the exponential function:

`f(x) = 0.1366 * 55^x`

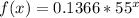
Now, to find f(2.5), simply substitute x = 2.5 into the equation:

`f(2.5) = 0.1366 * 55^2.5 ≈ 0.1366 * 1603.2623 ≈ 219.27` (rounded to the nearest hundredth)