Question

Find y if the point (5,y) is on the terminal side of theta and cos theta = 5/13

Answer 1

For this problem we have a point given (5,y) and we know that this point is on a terminal side of an angle, we also know that:

`\cos \theta=(5)/(13)`

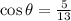
If we know the cos then we can find the sin on this way:

`\sin \theta=(y)/(13)`

Then we can apply the following identity from trigonometry:

`\sin ^2\theta+\cos ^2\theta=1`

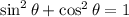
Using this formula we got:

`((5)/(13))^2+((y)/(13))^2=1`

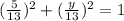
And we can solve for y:

`(y^2)/(169)=1-(25)/(169)=(144)/(169)`

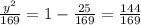
And solving for y we got:

`y=\sqrt{169\cdot(144)/(169)}=√(144)=\pm12`

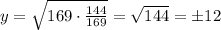
And the two possible solutions for this case are y=12 and y=-12