Question

Which term of AP, 100, 97, 94, 91,... will be its first negative term ?

Answer 1

Answer: -2 (which is the 35th term)

Step-by-step explanation

AP = "arithmetic progression", also known as "arithmetic sequence".

The AP starts at
`a_1 = 100` and has a common difference of d = -3. The negative common difference means we'll be decreasing by 3 each time.

Let's find the nth term.

`a_n = a_1 + d(n-1)\\\\a_n = 100 + (-3)(n-1)\\\\a_n = 100 - 3n + 3\\\\a_n = -3n + 103\\\\`

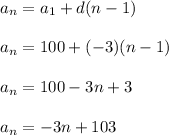
So for instance, when n = 4, we have:

`a_n = -3n + 103\\\\a_4 = -3*4 + 103\\\\a_4 = 91\\\\`

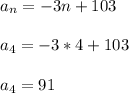
It tells us the 4th term of the AP is 91, which matches with what the teacher provided. I'll let you check the other terms.

The question is now: When is
`a_n` going to become a negative number?

We can follow these steps to find out

`a_n < 0\\\\-3n + 103 < 0\\\\103 < 3n\\\\3n > 103\\\\n > 103/3\\\\n > 34.33333 \ \text{ approximately}\\\\n > 34 \\\\`

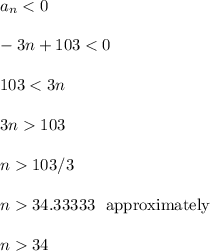
Let's see what happens if n = 34.

`a_n = -3n + 103\\\\a_(34) = -3(34) + 103\\\\a_(34) = 1\\\\`

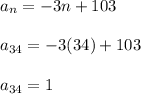
The 34th term is 1.

What about if n = 35?

`a_n = -3n + 103\\\\a_(35) = -3(35) + 103\\\\a_(35) = -2\\\\`

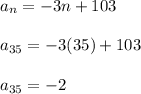
This is when we finally start to dip into negative territory.

The 35th term is the first negative term.

The 35th term is -2