We want to find the best prediction of the average number of hours a person spends at work every week if that person spends an average of 10 hours on recreational activities every week.
We will construct a line that adapts to the system by simple linear regression, and then we will find the x-value that makes the line take y=10.
First, we have the data:
We remember that in a simple regression model, we want to write an equation of the form:
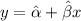
where:
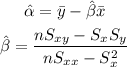
And the Sx, Sy and Sxx are the sums over all the x-values, the y-values and the multiplication of the x-values and y-values (respectively).
We will find those values:
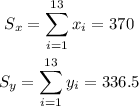
Also, we have:
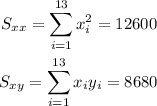
And applying the formula, having in mind that n=13, we get:
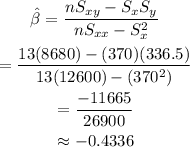
And, for alpha:
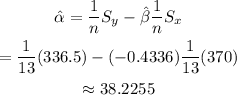
This means that the linear regression equation will be:
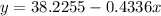
For finding the x-value that will have 10 hours of recreational activities, we replace the 10 value on y, and clear out the variable x:
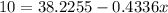
And thus,
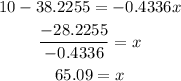
This means that when a person works 65 hours approximately, he will have 10 hours of recreational activities every week.