Question

A vendor is selling safety supplies. Flashlights cost $6.50 each, and batteries cost $1.50 per each. Select all the combinations of flashlights and batteries that the vendor could sell for exactly $26.00.

Answer 1

`\bold{ANSWER:}`
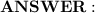
4 Flashlights
10 Batteries


`\bold{SOLUTION:}`

Let's assume the number of flashlights is "x"
and the number of batteries is "y".

The cost of x flashlights is 6.50x.
The cost of y batteries is 1.50y.

According to the problem, the total cost should be $26.00, so we can write the equation:

6.50x + 1.50y= 26.00

Now, let's find all the possible combinations of x and y that satisfy this equation.

One possible combination is:
- 4 flashlights (x = 4) and 10 batteries (y = 10)

Let's check if this combination satisfies the equation: 6.50(4) + 1.50(10) = 26.00
26.00 + 15.00 = 26.00
26.00
26.00

Since the equation is satisfied, the combination of 4 flashlights and 10 batteries is valid.

Another combination could be:
- 10 flashlights (x = 10) and 4 batteries (y = 4)

Let's check if this combination satisfies the equation: 6.50(10) + 1.50(4) = 26.00
65.00 +6.00 = 26.00
71.00 26.00

Since the equation is not satisfied, the combination of 10 flashlights and 4 batteries
is not valid.

Therefore, the only combination that satisfies the equation and costs exactly $26.00 is 4 flashlights and 10 batteries.