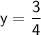Question

What is the value of y in simplest form?

Answer 1

`\sf y = (3)/(4)`

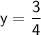
Explanation:

Given:

The point
`P = \left( (√(7))/(4),y\right)` lies on the unit circle.

To find:

Value of y

Solution:

In order t determine the value of y for the point P lying on the unit circle with center (0, 0) and radius 1, we can use the equation of a circle:

`\sf x^2 + y^2 = r^2`

In this case, r = 1 (since it's the unit circle), and we have the x-coordinate
`\sf x = (√(7))/(4)`

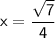
Now

Substitute in these values and solve for y:

`\sf \left((√(7))/(4)\right)^2 + y^2 = 1`

`\sf (7)/(16) + y^2 = 1`

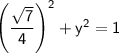
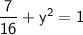
Now, isolate y² by subtracting (7/16) from both sides:

`\sf y^2 = 1 - (7)/(16)`

`\sf y^2 =( 1 \cdot 16 -7)/(16)`

`\sf y^2 = (9)/(16)`

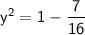
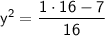
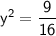
Take the square root of both sides:

`\sf√( y^2 )=\sqrt{ (9)/(16)}`

`\sf y = \pm (3)/(4)`

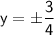
Since y lies in first quadrant. So, the value of y must be positive.

Therefore,

So, the value of y for the point P in simplest form is:

`\sf y = (3)/(4)`