Question

Find the area of the triangle with vertices A= (1,2,3),B=(2,4,7) and C=(3,3,4).

Answer 1

Answer: approximately 3.937 square units

Step-by-step explanation

Use the 3D version of the distance formula to determine how far it is from A(1,2,3) to B(2,4,7). This will get us the length of segment AB.

`A = (x_1,y_1,z_1) = (1,2,3) \ \text{ and } \ B = (x_2,y_2,z_2) = (2,4,7)\\\\d = √((x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2)\\\\d = √((1-2)^2+(2-4)^2+(3-7)^2)\\\\d = √((-1)^2+(-2)^2+(-4)^2)\\\\d = √(1+4+16)\\\\d = √(21)\\\\d \approx 4.5825757\\\\`

Segment AB is exactly
`√(21)` units long, which approximates to around 4.5825757.

Follow similar steps to find segments BC and AC have lengths of
`√(11) \approx 3.3166248` units and
`√(6) \approx 2.4494897` units respectively.

--------------

We have a triangle with these side lengths

`a = √(21)\approx4.5825757\\b = √(11) \approx 3.3166248\\c = √(6)\approx 2.4494897\\`

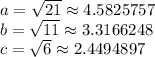
Compute the semi-perimeter. Add up the sides and divide in half.

`s = (a+b+c)/(2)\\\\s = (√(21)+√(11)+√(6))/(2)\\\\s \approx 5.1743451\\\\`

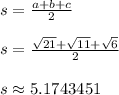
We'll use the values of a, b, c, and s to compute the area of the triangle using Heron's Formula.

`\text{area} = √(s(s-a)(s-b)(s-c))\\\\\text{area} \approx \sqrt{5.1743451(5.1743451-√(21))(5.1743451-√(11))(5.1743451-√(6))}\\\\\text{area} \approx 3.9370038599\\\\\text{area} \approx 3.937\\\\`

The area of the triangle is approximately 3.937 square units.

Round this approximate value however your teacher instructs.