Answer:
Solving simultaneous equations:
5x² - 2y² = 2 -----------(I)
2x - y = 1 ---------------(II)
In the second equation, isolate 'y'.
2x = 1 + y
2x - 1 = y
y = 2x -1 --------------(III)
Now, substitute y = 2x - 1 in equation (I).
5x² - 2(2x - 1)² = 2
Expand (2x- 1)² using the algebraic identity (a - b)² = a² -2ab + b²
5x² - 2(4x² - 4x + 1) = 2
Open the parenthesis by multiplying each term of (4x² - 4x + 1) by (-2).
5x² - 8x² + 8x - 2 = 2
Combine like terms.
-3x² + 8x - 2 -2 = 0
-3x² + 8x - 4 = 0
Multiply the entire equation by (-1).
3x² - 8x + 4 = 0
Sum = -8 & product = 12
Factors are -2 & -6. When we multiply (-2) & (-6), we get 12 and, when we add (-2) & (-6), we get (-8).
Rewrite the middle term using the factors.
3x² - 6x - 2x + 4 = 0
3x(x - 2) - 2(x - 2) = 0
(x - 2) (3x - 2) = 0
x - 2 = 0 ; 3x - 2 = 0
x = 2 ;
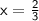
Plugin x = 2 in equation (III),
y = 2*2 - 1
= 4 - 1
= 3
Plugin x = 2/3 in equation (III),
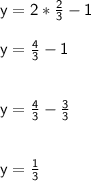
Answer:
