Question

Write a quadratic function in standard form containing the point (6,5) and x-intercepts 5 and 11.​

Answer 1

`\bold{ANSWER:}`
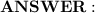
f(x) = -x^2 + 16x - 55.



`\bold{SOLUTION:}`

• To write a quadratic function in standard form, we can use the factored form of a quadratic equation:

f(x) = a(x - r1)(x − r2),

• where r1 and r2 are the x-intercepts. We are given that the x-intercepts are 5 and 11, so we can substitute these values into the equation:

f(x) = a(x-5)(x - 11).

• Now, we need to find the value of 'a' and substitute the coordinates of the given point (6, 5) to solve for 'a'.

• Substituting the point (6, 5) into the equation, we get:

5a(65) (6 - 11).

• Simplifying further:

5 = a(1)(-5).

5 = -5a

• Dividing both sides by -5

a = -1

• Now that we have found the value of 'a', we can substitute it back into the equation:
f(x)=-1(x-5)(x - 11).

• Expanding the equation:

f(x) = -1(x^2 - 11x - 5x + 55).

• Simplifying:

f(x) = -x^2 + 16x - 55.

Therefore,

The quadratic function in standard form that contains the point (6, 5) and x-intercepts 5 and 11 is:

f(x) = -x^2 + 16x - 55.

Answer 2

`\sf y = -x^2 + 16x - 55`

Explanation:

In order to write a quadratic function in standard form, we can use the factored form of a quadratic equation and then expand it.

The factored form of a quadratic equation is:

`\sf y = a(x - r_1)(x - r_2)`

Where:

• (r1, 0) and (r2, 0) are the x-intercepts.
• (6, 5) is a point on the quadratic function.

Given that the x-intercepts are 5 and 11, we can write:

y = a(x - 5)(x - 11)

Now, we'll use the point (6, 5) to find the value of 'a':

5 = a(6 - 5)(6 - 11)

5 = a(1)(-5)

5 = -5a

Now, solve for 'a' by dividing both sides by -5:

`\sf a =(-5)/(5)`

a = -1

Now that we have the value of 'a', you can write the quadratic function in standard form:

y = -1(x - 5)(x - 11)

Now, expand and simplify the expression:

`\sf y = -1(x^2 - 16x + 55)`

`\sf y = -x^2 + 16x - 55`

So, the quadratic function in standard form containing the point (6, 5) and x-intercepts 5 and 11 is:

`\sf y = -x^2 + 16x - 55`