Question

One side of a rectangle is 30 km longer than five times another side. Find the length of the sides, given that the area of the rectangle is 360 km2. Enter both sides, separated by a comma.

Answer 1

`\bold{ANSWER:}`
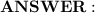
6 km & 60 km


`\bold{SOLUTION:}`

Let's assume that one side of the rectangle is x km.

• According to the problem, the other side is 30 km longer than five times the first side. Therefore, the length of the other side is (5x + 30) km.

• The area of a rectangle is given by the formula: Area = length x width.

• In this case, the area is given as 360 km2, so we can set up the equation:

360 = x x (5x + 30)

• Now, let's solve this equation to find the values of x:

360 = 5x^2 + 30x

• Rearranging the equation:

5x^2 + 30x - 360 = 0

• Dividing the entire equation by 5:

x^2+6x - 72 = 0

• Now, we can solve this quadratic equation by factoring or using the quadratic formula. Factoring the equation, we get:

(x+12)(x-6)= 0

• Setting each factor equal to zero:

x+12=0 or x-6=0

• Solving for x, we find:

x= -12 or x = 6

• Since the length of a side cannot be negative, we discard the solution x = -12.

• Therefore, the length of one side of the rectangle is 6 km.

• Using this value, we can find the length of the other side:

• Length of the other side = 5x + 30
=5(6) + 30
= 30 + 30
= 60 km

So, the lengths of the sides of the rectangle are 6 km and 60 km.