Question

Express

`2 ^( - 7)`
using a positive exponent.​

Answer 1

`(1)/(2^7)`

Explanation:

To express the number 2⁻⁷ with a positive exponent, we'll make use of the properties of exponents and their relationship with reciprocals.

`\hrulefill`

Here's a list of the exponent properties:

`\boxed{\left\begin{array}{ccc}\text{\underline{Properties of Exponents:}}\\\\1.\ a^0=1\\\\2.\ a^m * a^n=a^(m+n)\\\\3.\ a^m / a^n \ ((a^m)/(a^n) )=a^(m-n)\\\\4.\ (ab)^m=a^mb^m\\\\5.\ (a/b)^m=a^m/b^m\\\\6.\ (a^m)^n=a^(mn)\\\\7.\ a^(-m)=1/a^m\\\\8.\ a^(m/n)=(\sqrt[n]{a} )^m\end{array}\right}`

In our case, we will use the reciprocal identity (#7 on the table above).

`a^(-m)=(1)/(a^m) \\\\\\\\\therefore 2^(-7)=\boxed{(1)/(2^7) }`

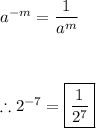
Thus, we can represent 2⁻⁷ as a positive exponent .