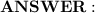
0.25 or 25%
• Let's denote the event that a tree is infected with root rot as R, and the event that it has bark disease as B.
• We are given the following information:
P(B') = 0.4 (the probability that a tree does not have bark disease)
P(R) = ? (the probability that a tree has root rot)
• Since the presence of root rot is independent of the presence of bark disease, we can use the
complement rule to find P(B), the probability that a tree has bark disease:
P(B) = 1 - P(B') = 1 − 0.4 = 0.6
• Now, we know that there is a 70% chance that a tree is infected with either root rot or bark disease. We can express this as the union of events R and B: P(RUB) = 0.7
• Using the addition rule for probability, we can rewrite P(R u B) as:
P(R) + P(B) = P(Rn B) = 0.7
• Since R and B are independent, P(R n B) = P(R) *
P(B). Therefore, we have:
P(R) + 0.6 - P(R) * 0.6 0.7
• Simplifying the equation, we get:
0.4P(R) = 0.1
• Dividing both sides by 0.4, we find:
P(R) = 0.1 / 0.4 = 0.25
Therefore,
The probability that a tree has root rot is 0.25 or 25%