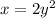the correct equation that can be simplified to find the inverse of
 is:
is:
![\[ x = 2y^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8zrhleetyuve6e5hqtapjxn9pa0fuxhasz.png)
Therefore, option D is correct
To find the inverse of a function, you swap the
 and
and
 variables and then solve for the new
variables and then solve for the new
 . The original function is
. The original function is
 . Let's go through the steps to find its inverse:
. Let's go through the steps to find its inverse:
1. Replace
 with
with
 :
:
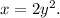
2. Solve for
 to get the inverse function.
to get the inverse function.
We'll proceed with these steps to find the correct equation that can be simplified to find the inverse of the given function.
The steps to find the inverse function yield two potential solutions because the original function is quadratic:
![\[ y = \pm (√(2))/(2) √(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7bjv1gf8i8nnc7s4vg22d1gx2o7ws9ll1x.png)
However, since the original function
 only considers the positive square root (as the square of a real number is always non-negative), we take the positive solution for the inverse function:
only considers the positive square root (as the square of a real number is always non-negative), we take the positive solution for the inverse function:
![\[ y = (√(2))/(2) √(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/84h92p851qsri9acwbadv0fukrpp0632ns.png)
This simplifies to:
![\[ y = \sqrt{(x)/(2)} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qxb9kc9o4t69b0na05jmreow9sgd7gvhxe.png)
Therefore, the correct equation that can be simplified to find the inverse of
 is:
is:
![\[ x = 2y^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8zrhleetyuve6e5hqtapjxn9pa0fuxhasz.png)
This matches the option:
O