First item:
When a relation is presented as a set of ordered pairs (a,b) its domain is given by all the different values that appear in the first coordinate of the pairs. Analogously its range is given by all the different values that appear in the second coordinate. For example, if we have the following relation:
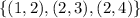
There are only two different values in the first coordinate of the pairs: 1 and 2. Then its domain is {1,2}.
There are three different values in the second coordinate of the pairs: 2, 3 and 4. Then its range is {2,3,4}.
Second item:
When the relation is presented in a mapping diagram we have something like this:
Each ellipse represents a set. The set from which the arrows come from is the domain and that at which the arrows arrive is the range. So for the relation shown in the picture its domain is {a,b,c,d} and its range is {x,y,z}
Third item:
When the relation is presented as a graph in a grid the domain will be given for all the values in the horizontal axis for which there's a corresponding value in the graph. If you draw a vertical line that passes through a value A in the horizontal axis you can find two cases:
- The line meets the graph at least once. Then A is part of the domain.
- The line never meets the graph. Then A is not part of the domain.
Something very similar happens with the range. The values that are part of the range are values in the vertical axis for which there's at least one corresponding value in the graph. If you draw a horizontal line that passes through a value B in the vertical axis you have:
- The line meets the graph at least once. Then B is part of the range.
- The line never meets the graph. Then B is not part of the range.