Question

Solve the equation 4x2 + 8x + 1 = 0 by completing the square.

Answer 1

Let's compare the given equation with the notable product below:

`(a+b)^2=a^2+2ab+b^2`

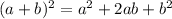
Since the first term is 4x², we have a = 2x.

Then, the second term is 8x, so since a = 2x, we have b = 2, this way 2ab = 8x

Now, since b = 2, we have b² = 4.

The constant term is just 1, so we need to add 3 units:

`\begin{gathered} 4x^2+8x+1+3-3=0 \\ 4x^2_{}+8x+4-3=0 \\ (2x+2)^2=3 \\ 2x+2=\pm\sqrt[]{3} \\ 2x=-2\pm\sqrt[]{3} \\ x=\frac{-2\pm\sqrt[]{3}}{2} \end{gathered}`

Therefore the correct option is the third one.