Question

Which table shows a proportional relationship between x and y ?

Answer 1

Table C

Explanation:

Given

Table A to D

Required

Which shows a proportional relationship

To do this, we make use of:

`k = (y)/(x)`

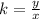
Where k is the constant of proportionality.

In table (A)

x = 2, y = 4

`k = (y)/(x)`

`k = (4)/(2)`

`k = 2`

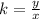
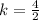
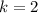
x = 4, y = 9

`k = (y)/(x)`

`k = (9)/(4)`

`k = 2.25`

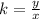
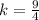
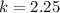
Both values of k are different. Hence, no proportional relationship

In table (B)

x = 3, y = 4

`k = (y)/(x)`

`k = (4)/(3)`

`k = 1.33`

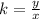
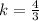
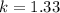
x = 9, y = 16

`k = (y)/(x)`

`k = (16)/(9)`

`k = 1.78`

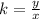
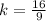
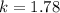
Both values of k are different. Hence, no proportional relationship

In table (C):

x = 4, y = 12

`k = (y)/(x)`

`k = (12)/(4)`

`k = 3`

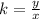
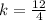
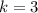
x = 5, y = 15

`k = (y)/(x)`

`k = (15)/(5)`

`k = 3`

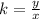
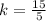
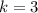
x = 6, y = 18

`k = (y)/(x)`

`k = (18)/(6)`

`k = 3`

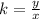
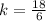
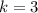
This shows a proportional relationship because all values of k are the same for this table