Question

An expression for the area of a shape is 6(a + 5) cm² Work out the area when a = –2,

Answer 1

when
`\(a = -2\)`, the area of the shape is
`\(18 \, \text{cm}^2\)`.

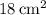when the area is 54 cm², the value of
`\(a\)` is 4.

To find the area of the shape when
`\(a = -2\)`, you can simply substitute the value of \(a\) into the given expression and then calculate it step by step. The expression for the area is
`\(6(a + 5) \, \text{cm}^2\)`.

1. Start by substituting
`\(a = -2\)` into the expression:

Area =
`\(6(-2 + 5) \, \text{cm}^2\)`

2. Now, simplify the expression inside the parentheses:

Area =
`\(6(3) \, \text{cm}^2\)`

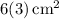
3. Multiply 6 by 3:

Area =
`\(18 \, \text{cm}^2\)`

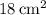
So, when
`\(a = -2\)`, the area of the shape is
`\(18 \, \text{cm}^2\)`.

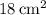To find the value of
`\(a\)` when the area is 54 cm², you can use the expression for the area:
`\(6(a + 5) \`,
`\text{cm}^2\)`, and set it equal to 54 cm², then solve for \(a\). Here's how you can do it step by step:

`\[6(a + 5) = 54\, \text{cm}^2\]`

1. Divide both sides of the equation by 6 to isolate
`\(a)`:

`\[(6(a + 5))/(6) = (54)/(6)\]`

This simplifies to:

`\[a + 5 = 9\]`

2. Now, subtract 5 from both sides of the equation to solve for
`\(a\)`:

`\[a = 9 - 5\]`

3. Calculate the value of
`\(a\)`:

`\[a = 4\]`

So, when the area is 54 cm², the value of
`\(a\)` is 4.

the complete Question is given below:

An expression for the area of a shape is 6(a + 5) cm² Work out the area when a = –2, b. the value of a when the area is 54 cm2