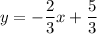Question

What is the equation of the line that passes through (4, -1) and (-2, 3)?

Answer 1

3--1/-2-4=4/-6=2/-3

y=-2/3x+b

-2*-2/3=4/3

3-4/3=5/3

y=-2/3x+5/3

Explanation:

Answer 2

`\displaystyle y=-(2)/(3)x+(5)/(3)`

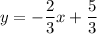
Explanation:

We want to find the equation of the line that passes through the two points:

(4, -1) and (-2, 3).

First, we will find the slope of the two points. So:

`\displaystyle m=(3-(-1))/(-2-4)=(4)/(-6)=-(2)/(3)`

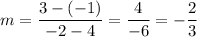
Now, we will use the point-slope form given by:

`y-y_1=m(x-x_1)`

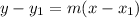
Use either point. I'm going to use (4, -1). So, substitute:

`\displaystyle y-(-1)=-(2)/(3)(x-(4))`

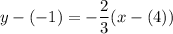
Simplify and distribute:

`\displaystyle y+1=-(2)/(3)x+(8)/(3)`

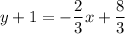
Subtract 1 from both sides. Therefore:

`\displaystyle y=-(2)/(3)x+(5)/(3)`