Answer:
Acceleration = 129.56 (2 d.p.)
Explanation:
To find the acceleration of the position function x(t) = sin(2t² + 5t) at t = 2 seconds, we need to take the second derivative of the position function with respect to time (t) and then evaluate it at t = 2 seconds.
To find the first derivative of x(t) with respect to t, use the chain rule for differentiation.
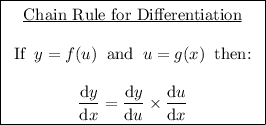

Differentiate the two parts separately:


Put everything back into the chain rule formula:


Substitute back in u = 2t² + 5t:

So, the first derivative, which represents the velocity function, is:

To find the second derivative of x(t) with respect to t, use the product rule for differentiation.



Put everything into the product rule formula:



So, the second derivative, which represents the acceleration function, is:

Now, evaluate x''(t) at t = 2 seconds:








Therefore, the acceleration of a position function x(t) = sin(2t² + 5t) at t = 2 seconds is 129.56 (rounded to two decimal places).