Question

Exactly as the image says. Thanks! :)

Answer 1

`p(x) = (1)/(16)(x+1)^2 (x-4)^2 (x-1)(x-2)^3`

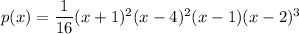
Explanation:

From observation of the given graph:

• The roots are at x = -1, x = 1, x = 2 and x = 4.
• The y-intercept is at y = 8.

When a root has a multiplicity of two, it means that the graph of the polynomial function touches or "bounces off" the x-axis at that particular value of x without crossing it. Therefore, from observation of the given graph, the values of x where the multiplicity of the root is two are x = -1 and x = 4.

When a root has a multiplicity of one, it means that the graph of the polynomial function crosses the x-axis at that particular value of x. The concavity of the graph remains the same as it approaches and passes through the x-axis. Therefore, from observation of the given graph, the value of x where the multiplicity of the root is one is x = 1.

When a root has a multiplicity of three, the graph of the polynomial has "cubic" behavior at the x-axis. It resembles a flattened "S" shape that crosses the x-axis at the cubic's center. All cubic functions undergo a single change in concavity (from concave down to concave up, or from concave up to concave down) and this change always occurs at the cubic's center. Therefore, from observation of the given graph, the value of x where the multiplicity of the root is three is x = 2.

Therefore, a possible factored form of the graphed function is:

`p(x) = (x+1)^2 (x-4)^2 (x-1)(x-2)^3`

The degree of a polynomial is determined by the highest exponent of the variable when the polynomial is fully expanded. When the polynomial is fully expanded, the highest exponent is equal to the sum of the exponents of the factors. Therefore:

`2 + 2 + 1 + 3 = 8`

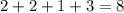
So the degree of this polynomial is 8, matching the given parameters.

To find the constant of the expanded function (y-intercept), we calculate the product of the constants of each factor raised to the exponent of the factor:

`1^2 \cdot (-4)^2 \cdot (-1) \cdot (-2)^3=128`

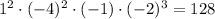
Since the y-intercept of the graphed function is 8, we need to adjust the constant by dividing the function by 16, as 128/16 = 8.

Therefore, the equation of the graphed function is:

`p(x) = (1)/(16)(x+1)^2 (x-4)^2 (x-1)(x-2)^3`

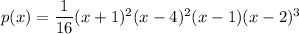
This equation satisfies the observed characteristics of the graph and the given y-intercept.