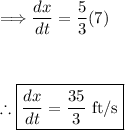Question

A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 7 ft/s along a straight path. How fast is the tip of his shadow moving when he is 50 ft from the pole?

Answer 1

35/3 ft/s

Explanation:

We want to determine the rate at which the tip of a man's shadow moves as he walks away from a streetlight. By using similar triangles, we can set up a relationship between the various lengths involved and then differentiate with respect to time.

`\hrulefill`

Create a diagram. Refer to the attached image.

Using the properties of similar triangles, we have:

`(DC)/(BC) =(DE)/(AB) \\ \\ \\ \\ \Longrightarrow (x-y)/(x) =(6)/(15)\\\\\\\\\Longrightarrow x-y=(2)/(5)x\\\\\\\\\Longrightarrow 5x-5y=2x\\\\\\\\\Longrightarrow 3x=5y\\\\\\\\\therefore x=(5)/(3)y`

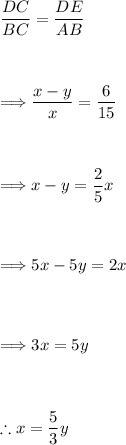
Taking the equation from above and differentiating with respect to time:

`\Longrightarrow (dx)/(dt)=(5)/(3)\Big((dy)/(dt)\Big)`

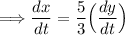
We are given dy/dt = 7 ft/s. Plug this in to find dx/dt:

`\Longrightarrow (dx)/(dt)=(5)/(3)(7)\\\\\\\\\therefore \boxed{(dx)/(dt)=(35)/(3) \ \text{ft/s}}`