Question

The length of a side of a square is 5 + 2 units. If the perimeter is 48 units, complete the following

a. Write an equation to represent this information.
b. Solve for z
c. What is the area of the square?

Answer 1

Explanation:

The length of a side of a square is 5 + 2 units. If the perimeter is 48 units, complete the following

I will assume you MEANT 5z+ 2 units

The perimeter of a SQUARE is 4 times the side length

4 ( 5z + 2) = 48 divide both sides by '4'

5z+ 2 = 12 subtract 2 from both sides

5z = 10 units

z = 2 units ( so side length = 12 units)

Area of a SQUARE = side length x side length = 12 x 12 = 144 units^2

Answer 2

Part a: equation: 4(5z + 2) = 48

Part b: z = 2

Part c: Area : 144 square units

Explanation:

Part a:

The perimeter of a square is the total length of all four sides of the square. Since each side of the square is 5z + 2 units long, the perimeter is:

Perimeter = 4 × (5z + 2)

We know that the perimeter is 48 units, so we can set up the following equation:

4(5z + 2) = 48

4(5z + 2) = 48Part b:

To solve for z, we can divide both sides of the equation by 4:

`\sf (4(5z + 2) )/(4)=( 48)/(4)`

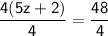
5z + 2 = 12

Subtracting 2 from both sides of the equation, we get:

5z + 2 - 2 = 12 - 2

5z = 10

Dividing both sides of the equation by 5, we get:

`\sf (5z )/(5)=( 10)/(5)`

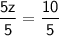
z = 2

z = 2Part c:

The area of a square is the length of one side of the square multiplied by itself. Since each side of the square is 5z + 2 units long, the area of the square is:

Area = (5z + 2)²

Substituting z = 2 into the equation, we get:

Area = (5 × 2 + 2)²

Evaluating the expression, we get:

Area = (12)²

Area = 144 square units

Therefore, the area of the square is 144 square units.