Question

What are the zeros of the polynomial function? f(x)=x4−2x3−103x2 200x 300 select each correct answer.

Answer 1

To find the zeros of the polynomial function f(x) =
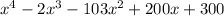`x^(4) - 2x^(3) - 103x^(2) + 200x + 300`, one must use numerical methods or factoring techniques, since it is a fourth-degree polynomial. A graphing calculator or the Rational Root Theorem may assist in finding rational zeros. For any quadratic part of the polynomial, the zeros can then be determined using the quadratic formula.

Step-by-step explanation:

To find the zeros of the polynomial function f(x) =
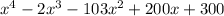`x^(4) - 2x^(3)- 103x^(2) + 200x + 300`, we have to solve the polynomial equation by setting f(x) equal to zero. The zeros of the polynomial are the values of x that make the equation true. Since it's a fourth-degree polynomial, there can be up to four real zeros, though some might be repeated or non-real complex numbers. Solving such a high-degree polynomial analytically can be complex, often requiring numerical methods or factoring if the roots are rational.

For this specific problem, unless the roots are easily factorizable or recognizable, a numerical method such as using the Rational Root Theorem, synthetic division, or a graphing calculator would be practical. If one or two real zeros are found, they can be used to reduce the polynomial order and the remaining zeros can be found using the quadratic formula for any resulting quadratic parts of the polynomial.

If we had a quadratic function of the form
`ax^(2)` + bx + c = 0, solving for the zeros would be more straightforward as we'd use the quadratic formula x = (-b ± √(
`b^(2)` - 4ac))/(2a). However, this particular polynomial is more complex due to its degree.