Answer:
Approximately
 .
.
Step-by-step explanation:
In a double slit diffraction, depending on which of the two slit each ray comes from, rays reaching the same position on the screen might have travelled a different distance. This distance is referred to as the path difference.
To produce a bright line at a certain position on the screen, the two rays arriving at that position need to be in phase. The path difference between these two rays would need to be an integer multiple of the wavelength. If the wavelength of the light is
 , these bright lines would appear at positions where the path difference is
, these bright lines would appear at positions where the path difference is
 for integers
for integers
 ,
,
 , etc.
, etc.
For example, a path difference of
 (for which
(for which
 ) would produce the first maximum. A path difference of
) would produce the first maximum. A path difference of
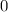 (where
(where
 ) would produce the bright line at the center of the screen, the central maximum.
) would produce the bright line at the center of the screen, the central maximum.
The following relation approximately holds for each bright line on the screen:
 ,
,
Where:
 is the distance between the two slits.
is the distance between the two slits.
 is the distance between this bright line and the central maximum, and
is the distance between this bright line and the central maximum, and
 is the distance between the screen and the slits.
is the distance between the screen and the slits.
This question suggests that the distance between each adjacent pair of bright lines on the screen is approximately
 . Hence, for the first maximum, the distance from the central maximum would be:
. Hence, for the first maximum, the distance from the central maximum would be:
 .
.
The path difference that produced the first maximum (
 ) is:
) is:
 .
.
Rearrange the equation to approximate the distance between the two slits:
 .
.
Apply unit conversion and ensure that all quantities are measured in standard units:
 .
.
 .
.
Substitute in
 ,
,
 , and
, and
 to find the distance between the two gaps:
to find the distance between the two gaps:
 .
.