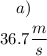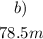Question

So I have these kinematics questions and I’m having a hard time answering it. It says:While riding a hot air balloon, which is steadily descending at a speed of 2.52 m/s, you accidentally drop your cell phone.(a) After 4.00 s, what is the speed of the cell phone?(b) How far is the cell phone below the balloon after this time?(c) What are your answers to part (a) and (b) if the balloon id rising steadily at 2.52 m/s?

Answer 1

a)

Objects moving under free fall have a constant acceleration g, which is the gravitational acceleration, directed downwards:

`g=9.81(m)/(s^2)`

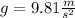
Since the balloon is descending at a speed of 2.52 m/s, the initial speed of the phone is 2.52 m/s. To find the speed after 4.00 seconds, use the formula that comes from the definition of acceleration:

`v_f=v_0+gt`

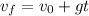
Substitute the value for each parameter:

`\begin{gathered} v_f=2.52(m)/(s)+(9.81(m)/(s^2))(4.00s) \\ =2.52(m)/(s^2)+39.24(m)/(s) \\ =41.76(m)/(s) \end{gathered}`

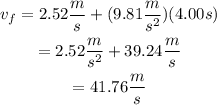
b)

From the reference frame of the balloon, the cellphone starts falling from rest, and accelerates with a constant acceleration g.

The equation that describes the distance traveled by an object that starts from rest and moves with constant acceleration g is:

`d=(1)/(2)gt^2`

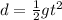
Substitute the values of g and t to find how far is the cell phone below the balloon after 4 seconds:

`\begin{gathered} d=(1)/(2)(9.81(m)/(s^2))(4.00s)^2 \\ =78.48m \end{gathered}`

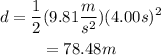
c)

If the balloon is rising steadly at 2.52 m/s instead of descending, then the acceleration of the cellphone will be directed in the opposite direction of its initial speed. Then, the initial speed and the acceleration must have opposite signs. Considering the upward direction as positive, we have that the initial speed of the phone is 2.52 m/s and its acceleration is -g. Then:

`\begin{gathered} v_f=(2.52(m)/(s))-(9.81(m)/(s))(4.00s) \\ =2.52(m)/(s)-39.24(m)/(s) \\ =-36.72(m)/(s) \end{gathered}`

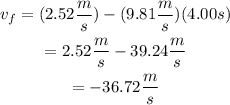
The speed is the modulus of the velocity. Then, the speed of the phone after 4 seconds in this situation, would be 36.72 m/s.

On the other hand, in the reference frame of the rising balloon, the phone still starts moving at rest and accelerating uniformly towards the floor. The answer will be the same, and the phone will be 78.48 m below the balloon after 4 seconds.

Therefore, the answers with the correct amount of significant figures, are:

a)

`41.8(m)/(s)`

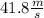
b)

`78.5m`

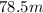
c)

`\begin{gathered} a) \\ 36.7(m)/(s) \end{gathered}`
`\begin{gathered} b) \\ 78.5m \end{gathered}`