Question

The graph of the polynomial function "f" is shown above, where -5 < x < 5. The function "f" has a local extrema at x = -2 and x = 2, and the graph of "f" has a point of infliction at x = 0.

a) what intervals is "f" increasing?

b) what intervals is the graph of "f" concave down?

Answer 1

Explanation:

Answer 2

a) f is increasing on the intervals
`(-5, -2) \cup (-2, 0) \cup (0, 2) \cup (2, 5)\).`

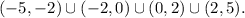
b) The graph of f is concave down on the intervals
`\((-5, 0) \cup (0, 5)\)`.

a) Intervals where f is Increasing:

The graph of f is increasing on intervals where the derivative
`\( f'(x) \)` is positive. Local minima and maxima occur where
`\( f'(x) = 0 \)` or is undefined.

Given that f has local extrema at x = -2 and x = 2 , and a point of inflection at x = 0, we can identify the intervals where f is increasing:

- (-5, -2): Before the local minimum at x = -2 , f'(x) > 0 .

- (-2, 0): Between the local minimum at x = -2 and the inflection point at x = 0 , f'(x) > 0 .

- (0, 2): Between the inflection point at x = 0 and the local maximum at x = 2 , f'(x) > 0.

- (2, 5) : After the local maximum at x = 2, f'(x) > 0 .

b) Intervals where the graph of f is Concave Down:

The graph of f is concave down on intervals where the second derivative f''(x) is negative.

- (-5, 0) : Before the inflection point at x = 0 , f''(x) < 0 .

- (0, 5): After the inflection point at x = 0 , f''(x) < 0 .

In summary:

a) f is increasing on the intervals
`(-5, -2) \cup (-2, 0) \cup (0, 2) \cup (2, 5)\).`

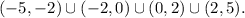
b) The graph of f is concave down on the intervals
`\((-5, 0) \cup (0, 5)\)`.