Question

I need help pls this is for today

Answer 1

2a. The max number of turning point on a polynomial with the m degree is m-1

In this case the answer is 3 because 4-1=3

2b.First, let apply Descartes Rule of Signs to find possible real zeroes.

First, find number of sign changes. There is one sign change so there is possible of one positive zero.

`- ( - x) {}^(4) + 7( - x) {}^(3) + 17( - x) {}^(2) + 9( - x)`

`- {x}^(4) - 7x {}^(3) + 17x - 9x`

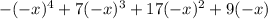
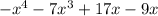
Now there is 2 sign changes so at max, we have 2 negative zeroes

So we have 1+2=3 possible real zeroes at max.

Now plug in (-x) a see how many sign changes occur here.

2c. Since the degree is 4, the zeroes at most will be 4. That is not always thr case if we have multiplicity of zero but at most, we will have four zeroes.

2d. Since this a even degree polynomial and it's negative,

as we go to the left and right, we will approach negative infinity

2e.Look at graph above

We have 3 zeroes like we said, there is 3 turning points, the end behavior is right so it like we did good.

2f. as x approaches -1 from the left, it increases to zero.