Question

Hello , how to do 6(iii)?

Answer 1

`\displaystyle (dS)/(dt)=(3)/(50r)`

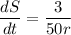
Explanation:

Water is being pumped into an inflated rubber sphere at a constant rate of 0.03 cubic meters per second.

So, dV/dt = 0.03.

We want to show that dS/dt is directly proportional to 1/r.

In other words, we want to establish the relationship that dS/dt = k(1/r), where k is some constant.

First, the volume of a sphere V is given by:

`\displaystyle V=(4)/(3)\pi r^3`

Therefore:

`\displaystyle (dV)/(dt)=4\pi r^2(dr)/(dt)`

Next, the surface area of a sphere S is given by:

`\displaystyle S=4\pi r^2`

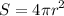
Therefore:

`\displaystyle (dS)/(dt)=8\pi r(dr)/(dt)`

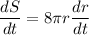
We can divide both sides by 2:

`\displaystyle (1)/(2)(dS)/(dt)=4\pi r(dr)/(dt)`

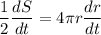
We can substitute this into dV/dt. Rewriting:

`\displaystyle (dV)/(dt)=r\Big(4\pi r(dr)/(dt)\Big)`

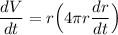
So:

`\displaystyle (dV)/(dt)=(1)/(2)r(dS)/(dt)`

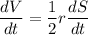
Since dV/dt = 0.03 or 3/100:

`\displaystyle (3)/(100)=(1)/(2)r(dS)/(dt)`

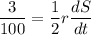
Therefore:

`\displaystyle (dS)/(dt)=(3)/(50r)=(3)/(50)\Big((1)/(r)\Big)`

Where k = 3/50.

And we have shown that dS/dt is directly proportional to 1/r.