Question

X is normally distributed with a mean of 100 and a standard deviation of 15. What is the probability of randomly sampling a score from X and having it be greater than or equal to 126 ​

Answer 1

Using calculator: 0.0415

Using Z-score Table: 0.0418

Explanation:

There are two ways you can solve this problem.

1. Use the normal distribution function on a calculator.

Entered values:

Lower Limit: 126

Upper Limit: 999999999999999... (To encompass all the data)

Standard Deviation: 15

Mean: 100

2. Find the Z score and look up probabilities on table.

Formula for Z score:

`Z=(x-mean)/(standard deviation) \\\\Z= (126-100)/(15)=1.7333...`

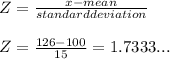
Z = 1.7333

This means that the value 126 is 1.733 standard deviations away from the mean. We can look this value up on the Z table to find its corresponding probability.

This will show us the probability of the random sampling being equal to or lower than 126.

P = 0.9582

So to find the probability of it being above, we simply just calculate the inverse as all probabilities on the curve = 1.

1-0.9582 = 0.0418

NOTE: Values found from the table will usually be a bit different from if you find it from a calculator, the one you need will depend on the method you use in class.

Hope this helped!