Question

The filament of a 100 w (120 v ) light bulb is a tungsten wire 0.035 mm in diameter. at the filament's operating temperature, the resistivity is 5.0×10−7ω⋅m .

Answer 1

The resistance of the tungsten filament in the 100 W (120 V) light bulb is approximately 14.4 ohms.

Step-by-step explanation:

The resistance (R) of a wire is given by the formula:

`\[ R = (\rho L)/(A) \]`

where:

- rho is the resistivity of the material (given as
`\(5.0 * 10^(-7) \, \Omega \cdot m\)),`

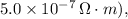
- L is the length of the wire (not provided),

- A is the cross-sectional area of the wire.

The cross-sectional area A can be calculated using the formula for the area of a circle:

`\[ A = \pi r^2 \]`

Given the diameter d of the wire as (0.035 , mm), the radius (r) is (0.0175 , mm).

Now, convert the radius to meters:

`\[ r = 0.0175 * 10^(-3) \, m \]`

Substitute r into the formula for A, then use A in the formula for R:

`\[ R = (5.0 * 10^(-7) \cdot L)/(\pi \cdot (0.0175 * 10^(-3))^2) \]`

Now, to find L, we can use the power equation
`\( P = V^2 / R \)`. Rearrange it to solve for R

`\[ R = (V^2)/(P) \]`

Substitute the given values for voltage ( V = 120 , V ) and power (( P = 100 , W )):

`\[ R = ((120)^2)/(100) \]`

Finally, equate the two expressions for ( R ) and solve for ( L ):

`\[ ((120)^2)/(100) = (5.0 * 10^(-7) \cdot L)/(\pi \cdot (0.0175 * 10^(-3))^2) \]`

Solving for ( L ) yields the length of the wire. Once the length is determined, substitute it back into the original formula for ( R ) to get the final resistance value.