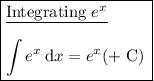Question

Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis. (Round your answer to three decimal places.)

Answer 1

1.066 (3 d.p.)

Explanation:

The volume of the solid formed by revolving a region, R, around a vertical axis, bounded by x = a and x = b, is given by:

`\displaystyle 2\pi \int^b_ar(x)h(x)\;\text{d}x`

where:

• r(x) is the distance from the axis of rotation to x.
• h(x) is the height of the solid at x (the height of the shell).

`\hrulefill`

We want to find the volume of the solid formed by revolving a region, R, around the y-axis, where R is bounded by:

`y=(1)/(√(2\pi))e^{-(x^2)/(3)}`

`y=0`

`x=0`

`x=1`

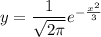
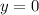
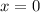
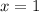
As the axis of rotation is the y-axis, r(x) = x.

Therefore, in this case:

`r(x)=x`

`h(x)=(1)/(√(2\pi))e^{-(x^2)/(3)}`

`a=0`

`b=1`

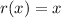
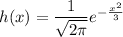
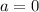
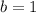
Set up the integral:

`\displaystyle 2\pi \int^(1)_0x \cdot(1)/(√(2\pi))e^{-(x^2)/(3)}\;\text{d}x`

Take out the constant:

`\displaystyle 2\pi \cdot (1)/(√(2\pi))\int^(1)_0x \cdot e^{-(x^2)/(3)}\;\text{d}x`

`\displaystyle √(2\pi)\int^(1)_0x \cdot e^{-(x^2)/(3)}\;\text{d}x`

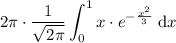
Integrate using the method of substitution.

`\textsf{Let}\;u=-(x^2)/(3)\implies \frac{\text{d}u}{\text{d}x}=-(2x)/(3)\implies \text{d}x=-(3)/(2x)\;\text{d}u`

`\textsf{When}\;x=0 \implies u=0`

`\textsf{When}\;x=1 \implies u=-(1)/(3)`

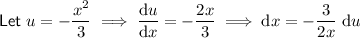
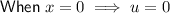
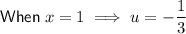
Rewrite the original integral in terms of u and du:

`\displaystyle √(2\pi)\int^{-(1)/(3)}_0x \cdot e^(u)\cdot -(3)/(2x)\;\text{d}u`

`\displaystyle √(2\pi)\int^{-(1)/(3)}_0 -(3)/(2)e^(u)\; \text{d}u`

`-(3√(2\pi))/(2)\displaystyle \int^{-(1)/(3)}_0 e^(u)\; \text{d}u`

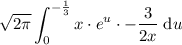
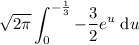
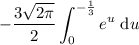
Evaluate:

`\begin{aligned}-(3√(2\pi))/(2)\displaystyle \int^{-(1)/(3)}_0 e^(u)\; \text{d}u&=-(3√(2\pi))/(2)\left[ \vphantom{\frac12}e^u\right]^{-(1)/(3)}_0\\\\&=-(3√(2\pi))/(2)\left[ \vphantom{\frac12}e^{-(1)/(3)}-e^0\right]\\\\&=-(3√(2\pi))/(2)\left[ \vphantom{\frac12}e^{-(1)/(3)}-1\right]\\\\&=1.06582594...\\\\&=1.066\; \sf (3\;d.p.)\end{aligned}`

Therefore, the volume of the solid is approximately 1.066 (3 d.p.).

`\hrulefill`

`\boxed{\begin{minipage}{3 cm}\underline{Integrating $e^x$}\\\\$\displaystyle \int e^x\:\text{d}x=e^x(+\;\text{C})$\end{minipage}}`