Question

Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis.

Answer 1

`(4096\pi)/(5)\approx 2573.593\; \sf (3\;d.p.)`

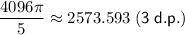
Explanation:

The shell method is a calculus technique used to find the volume of a solid revolution by decomposing the solid into cylindrical shells. The volume of each cylindrical shell is the product of the surface area of the cylinder and the thickness of the cylindrical wall. The total volume of the solid is found by integrating the volumes of all the shells over a certain interval.

The volume of the solid formed by revolving a region, R, around a vertical axis, bounded by x = a and x = b, is given by:

`\displaystyle 2\pi \int^b_ar(x)h(x)\;\text{d}x`

where:

• r(x) is the distance from the axis of rotation to x.
• h(x) is the height of the solid at x (the height of the shell).

`\hrulefill`

We want to find the volume of the solid formed by rotating the region bounded by y = 0, y = √x, x = 0 and x = 16 about the y-axis.

As the axis of rotation is the y-axis, r(x) = x.

Therefore, in this case:

`r(x)=x`

`h(x)=√(x)`

`a=0`

`b=16`

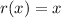
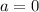
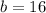
Set up the integral:

`\displaystyle 2\pi \int^(16)_0x√(x)\;\text{d}x`

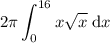
Rewrite the square root of x as x to the power of 1/2:

`\displaystyle 2\pi \int^(16)_0x \cdot x^{(1)/(2)}\;\text{d}x`

`\textsf{Apply the exponent rule:} \quad a^b \cdot a^c=a^(b+c)`

`\displaystyle 2\pi \int^(16)_0x^{(3)/(2)}\;\text{d}x`

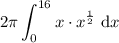
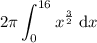
Integrate using the power rule (increase the power by 1, then divide by the new power):

`\begin{aligned}\displaystyle 2\pi \int^(16)_0x^{(3)/(2)}\;\text{d}x&=2\pi \left[(2)/(5)x^{(5)/(2)}\right]^(16)_0\\\\&=2\pi \left[(2)/(5)(16)^{(5)/(2)}-(2)/(5)(0)^{(5)/(2)}\right]\\\\&=2 \pi \cdot (2)/(5)(16)^{(5)/(2)}\\\\&=(4\pi)/(5)\cdot 1024\\\\&=(4096\pi)/(5)\\\\&\approx 2573.593\; \sf (3\;d.p.)\end{aligned}`

Therefore, the volume of the solid is exactly 4096π/5 or approximately 2573.593 (3 d.p.).

`\hrulefill`

`\boxed{\begin{minipage}{4 cm}\underline{Power Rule of Integration}\\\\$\displaystyle \int x^n\:\text{d}x=(x^(n+1))/(n+1)(+\;\text{C})$\\\end{minipage}}`