Question

A fancart of mass 0.8 kg initially has a velocity of < 0.9, 0, 0 > m/s. Then the fan is turned on, and the air exerts a constant force of < -0.2, 0, 0 > N on the cart for 1.5 seconds. 1. What is the change in momentum of the fancart over this 1.5 second interval?(kg*m/s) 2.What is the change in kinetic energy of the fancart over this 1.5 second interval? (J) Thank you it is due tonight!

Answer 1

Change in momentum:
`\langle -0.3,\, 0,\, 0\rangle\; {\rm kg \cdot m\cdot s^(-1)}`.

Change in kinetic energy: approximately
`(-0.2)\; {\rm J}`.

Step-by-step explanation:

Change in momentum
`\Delta p` is equal to the net impulse
`J` on the object. In order to find the net impulse
`J\!`, multiply the net force on the object
`F_{\text{net}` by the duration
`\Delta t`:

`\begin{aligned} J &= F_{\text{net}}\, \Delta t \\ &= (1.5)\, \langle -0.2,\, 0,\, 0\rangle\; {\rm N\cdot s} \\ &= \langle -0.3,\, 0,\, 0\rangle\; {\rm kg \cdot m\cdot s^(-1)} \end{aligned}`.

Since the change in momentum is equal to net impulse:

`\Delta p = J = \langle -0.3,\, 0,\, 0\rangle\; {\rm kg \cdot m\cdot s^(-1)}`.

Divide the change in momentum by mass
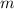`m` to find the change in velocity
`\Delta v`:

`\begin{aligned}\Delta v &= (\Delta p)/(m) \\ &= (\langle -0.3,\, 0,\, 0\rangle)/(0.8)\; {\rm m\cdot s^(-1)} \\ &\approx \langle -0.375,\, 0,\, 0\rangle\; {\rm m\cdot s^(-1)}\end{aligned}`.

Thus, velocity has changed from
`u = \langle 0.9,\, 0,\, 0\rangle\; {\rm m\cdot s^(-1)}` to:

`\begin{aligned} v &= u + \Delta v \\ &= \langle 0.9,\, 0,\, 0\rangle\; {\rm m\cdot s^(-1)} \\ &\quad + \langle -0.375,\, 0,\, 0\rangle\; {\rm m\cdot s^(-1)} \\ &= \langle 0.525,\, 0,\, 0\rangle\; {\rm m\cdot s^(-1)}\end{aligned}`.

The initial kinetic energy (a scalar) was:

`\begin{aligned}(\text{KE, initial}) &= (1)/(2)\, m\, _(2))^(2) \\ &\approx (1)/(2)\, (0.9^(2))\; {\rm J} \\ &=0.324\; {\rm J}\end{aligned}`.

The new kinetic energy would be:

`\begin{aligned}(\text{KE}) &= (1)/(2)\, m\, u\^(2) \\ &\approx (1)/(2)\, (0.525^(2))\; {\rm J} \\ &= 0.11025\; {\rm J}\end{aligned}`.

Hence, the change in kinetic energy would be:

`\begin{aligned} &(\text{KE}) - (\text{KE, initial}) \\ \approx\; & 0.324\; {\rm J} - 0.11025\; {\rm J}\\ \approx \; & (-0.2)\; {\rm J} \end{aligned}`.