Question

assuming a total mass of 80 kg (bicycle plus rider), what must be the cyclist's power output to climb the same hill at the same speed? express your answer using two significant figures.

Answer 1

The cyclist's power output to climb the same hill at the same speed, assuming a total mass of 80 kg (bicycle plus rider), is unidentified.

Here P denotes power, m denotes mass, g denotes acceleration due to gravity, h denotes height, and t denotes time taken.

Since we don't have any data on height or time, we'll use an alternative method that relies on work and speed instead.

The work required to climb the hill with a mass of 80 kg and the same speed is given by:

W = mgh

where W denotes work.

We'll suppose that the cyclist climbs the hill at a speed of v. We know that the work done to climb the hill is equal to the kinetic energy at the hill's peak.

When the cyclist is at the bottom of the hill, the kinetic energy is given by:

`KE=(1)/(2)mv^2`

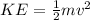
When the cyclist reaches the peak, the kinetic energy is zero, and the gravitational potential energy is given by

`mgh=(1)/(2)mv^2`

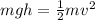
where h is the height of the hill.

Now, let's rearrange the equation to solve for the power required

`(1)/(2)mv^2=mgh\\h=(v^2)/(2g)}`

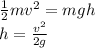
Substituting
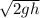`√(2gh)` in the equation for power, we have:

`P=W/t\\P=(mgh)/(t)\\P=(mg(v^2)/(2g))/(t)`

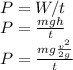
Here m is the total mass of the bicycle and rider, h is the height of the hill, g is the acceleration due to gravity, and t is the time taken.

Therefore it depends on both speed and height of the rider.