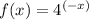Given:
There are given that the function:
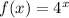
Step-by-step explanation:
To find any transformation, we need to use the parent function which is given.
Then,
(A): Shifted 4 units up:
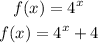
Hence, the new function is shown below:
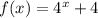
(B): Shifted 3 units down.
Then,
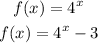
Hence, the new function is shown below:
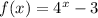
(C): Shifted 2 units left:
Then,
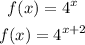
Hence, the new function is shown below:
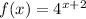
(D): Shifted 5 units right.

Hence, the new function is shown below:
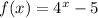
(E); Reflected about x-axis:
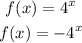
Hence, the new function is shown below:

(F): Reflected about the y-axis:
Then,
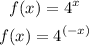
Hence, the new function is shown below: