Question

HelpClassify each number below as a rational number or as an irrational number

Answer 1

By definition:

- Rational numbers are those numbers that can be written as simple fractions. A fraction has this form:

`\begin{gathered} (a)/(b) \\ \end{gathered}`

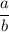
Where "a" is the numerator and "b" is the denominator. Both are Integers, and:

`b\\e0`

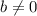
- Irrational numbers cannot be written as simple fractions.

Then, knowing those definitions, you can identify that:

1. The number:

`-\sqrt[]{25}=-5`

Since -5 is an Integer, it can be written as:

`=(-5)/(1)`

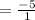
Therefore, it is a Rational Number.

2. You can identify that the second number is a Repeating Decimal because the line over the decimal digits indicates that its digits are periodic.

By definition, Repeating Decimals are Rational Numbers.

3. Notice that the next number is:

`-\sqrt[]{10}\approx-3.162278`

Since it cannot be written as a simple fraction, it is not a Rational Number.

4. For the number:

`-(18)/(5)`

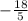
You can identify that it is a fraction whose numerator and denominator and Integers. Then, it is a Rational Number.

5. Notice that the last number is:

`18\pi`

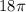
By definition, π is an Irrational Number.

Therefore, the answer is: