Question

Show that the function g(x)=x-2/5 is the inverse of f(x)=5x+2Step 1: the function notation f(x) can be written as a variable in an equation. Is that variable x or y?Write f(x)=5x+2 as an equation with the variable you chose above.Step 2: switch the variables in the equation from Step 1. Then solve for y. Show your work.Step 3: Find the inverse of g(x)= x-2/5. What does this tell you about the relationship between f(x)=5x+2 and g(x)? Show your work.

Answer 1

Given that :

`f(x)\text{ = 5x + 2}`

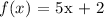
We can prove that :

`g(x)\text{ = }\frac{x\text{ -2}}{5}`

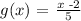
is it's inverse doing the following:

Step 1. Set y = f(x):

`y\text{ = 5x + 2}`

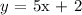
Step 2. Switch the variables:

`x\text{ = 5y + 2}`

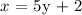
Then we solve for y:

`\begin{gathered} 5y\text{ = x - 2} \\ \text{Divide both sides by 5} \\ y\text{ = }\frac{x\text{ -2}}{5} \end{gathered}`

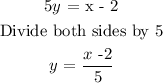
Step 3. The inverse of :

`g(x)\text{ = }(x-2)/(5)`

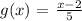
can be found in a similar way.

`\begin{gathered} y\text{ = }(x-2)/(5) \\ x\text{ = }(y-2)/(5) \\ \text{Cross}-\text{Multiply} \\ 5x\text{ = y -2} \\ y\text{ = 5x + 2} \end{gathered}`

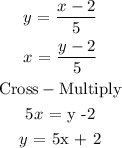
This tells us that f(x) and g(x) are one to one functions are f(x) is the mirror image of g(x)