Question

A box can be formed by cutting a square out of each corner of a piece of cardboard and folding the sides up. If the piece of cardboard is 78 cm by 78 cm and each side of the square that is cut out has length x cm, the function that gives the volume of the box is V=6084x−312x2+4x3. Complete parts (a) and (b) below.

Answer 1

a) Notice that:

1)

`6084x-312x^2+4x^3=4x(1521-78x+x^2)=4x(x-39)^2\text{.}`

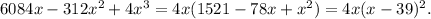
Therefore V(x)=0 at x=0 and it has a double root at x=39.

2)

`\begin{gathered} V(-1)=6084(-1)-312(-1)^2+4(-1)^3, \\ V(-1)=-6084-312-4<0. \end{gathered}`

Therefore, V(x)<0 when x is in the following interval:

`(-\infty,0).`

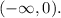
3)

`V(1)=6084(1)-312(1)^2+4(1)^3>0.`

Therefore, V(x)>0 when x is in the following set:

`(0,39)\cup(39,\infty).`

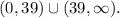
b) Since x is a length, then it must be greater than zero, also 2x must be smaller than 78, therefore the values of x that makes sense in the context are in the interval:

`(0,39)\text{.}`

Answer:

a) Option B) The values of x that makes V>0 are in the set:

`(0,39)\cup(39,\infty).`

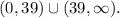
b) Option A) The values of x that give squares that can be cut out to construct a box are the interval:

`(0,39)\text{.}`

(0,39).