Question

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.

Match the absolute value functions with their vertices.
rights reserved
f(x)= |x-51+
f(x) = -2|2|-
-
f(x)= |x-1| +4
f(x)=x+11-4
Vertex
(-1,-4)
(5, 1)
(0, -1)
(2, 4)
f(x) = |z|-
f(2)=|z-|+{
Absolute Value Function

Answer 1

`\boxed {\left(-1, -(3)/(7)\right)} \longrightarrow \boxedf\left(x\right)\:=\:(1)/(2)\left`

`\boxed{\left(5,\:(2)/(3)\right)} \longrightarrow \boxedx\:-\:5\right`

`\boxed{\left(0,\:-(4)/(5)\right)} \longrightarrow \boxedx\right`

`\boxed{\left((2)/(5),\:(5)/(3)\right)} \longrightarrow \boxed+(5)/(3)`

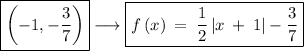
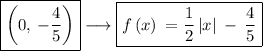
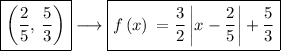
Explanation:

The vertex of an absolute function
y = f(x) = a|x - b| + c occurs at x - b = 0 or when x = b

Plugging this into the original equation will give the value for f(b) which will be f(b) = 0 + c which will be the y-value of the vertex

`\text{Vertex of } f(x) = (3)/(5) |x - 5| + (2)/(3)\\\\ \longrightarrow x = 5, y = (2)/(3) \\\\\longrightarrow \left(5, (2)/(3) \right)`

You can do the others in a similar manner.

Here it is easier because the constant in f(x) corresponds to the y-coordinate of the vertex and they are different in the answer choices